|
There are no translations available.
Признаки Рейнина с точки зрения математики
Автор - Олег Хрулёв  This e-mail address is being protected from spambots. You need JavaScript enabled to view it
Этот e-mail адрес защищен от спам-ботов, для его просмотра у Вас должен быть включен Javascript
This e-mail address is being protected from spambots. You need JavaScript enabled to view it
Этот e-mail адрес защищен от спам-ботов, для его просмотра у Вас должен быть включен Javascript  www.socionic.ru (администратор еще более 30 сайтов по соционике, в том числе и этого) www.socionic.ru (администратор еще более 30 сайтов по соционике, в том числе и этого)
Метод определения типа с помощью основных дихотомий Первые тесты как в соционике, так и в типологии Майерс-Бриггс использовали четыре основных дихотомии. При этом вопрос о надежности определения типа таким образом в MBTI, например, решается очень просто, то что определяет тест и есть тип. “Учение партии истинно, потому что оно верно”. Попробуем все же подвергнуть сомнению столь простой способ определения типа, и допустим, что вероятность правильного определения дихотомии p не обязательно равна 1. В данном случае мы предполагаем следующее: - Дихотомии определяются независимо.
- Для простоты рассмотрим случай, когда вероятности определение каждой из дихотомий равны между собой.
Важно заметить, что не делается никаких предположений: - О распределении типов в природе.
- О конкретном психологическом наполнении каждой из дихотомий.
- О конкретном способе определения каждой из дихотомий.
Тогда мы получаем n однородных, независимых опытов, событие А - правильное определение дихотомии, вероятность появления которого равно p, не появления q = 1-p. Из пункта 2 следует, что p остается одной и той же в каждом опыте. Тогда вероятность Рm,n того, что А в этих n опытах появится ровно m раз (0<=m<=n).
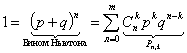 , где , где 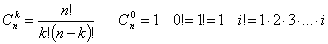
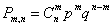 -биномиальное распределение. -биномиальное распределение.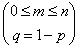
Если мы используем только основные дихотомии, то для правильного определения типа n = m = 4. Количество различных вариантов при типировании по четырем дихотомиям: Всего типов | Правильный тип | Ошибка в одной дихотомии | Ошибка в двух дихотомиях | Ошибка в трех дихотомиях | Ошибка в четырех дихотомиях | 16 | 1 | 4 | 6 | 4 | 1 | Следующая таблица показывает вероятность каждого из этих вариантов в процентах. По строкам в сумме может не получаться 100% из-за ошибок округления: Вероятность правильного определения каждой дихотомии p | Правильный тип | Ошибка в одной дихотомии | Ошибка в двух дихотомиях | Ошибка в трех дихотомиях | Ошибка в четырех дихотомиях | 100 | 100 | 0 | 0 | 0 | 0 | 99 | 96 | 3,8 | 0 | 0 | 0 | 98 | 92,2 | 7,5 | 0,2 | 0 | 0 | 97 | 88,5 | 10,9 | 0,5 | 0 | 0 | 96 | 84,9 | 14,1 | 0,8 | 0 | 0 | 95 | 81,4 | 17,1 | 1,3 | 0 | 0 | 94 | 78 | 19,9 | 1,9 | 0 | 0 | 93 | 74,8 | 22,5 | 2,5 | 0,1 | 0 | 92 | 71,6 | 24,9 | 3,2 | 0,1 | 0 | 91 | 68,5 | 27,1 | 4 | 0,2 | 0 | 90 | 65,6 | 29,1 | 4,8 | 0,3 | 0 | 89 | 62,7 | 31 | 5,7 | 0,4 | 0 | 88 | 59,9 | 32,7 | 6,6 | 0,6 | 0 | 87 | 57,2 | 34,2 | 7,6 | 0,7 | 0 | 86 | 54,7 | 35,6 | 8,6 | 0,9 | 0 | 85 | 52,2 | 36,8 | 9,7 | 1,1 | 0 | 84 | 49,7 | 37,9 | 10,8 | 1,3 | 0 | 83 | 47,4 | 38,8 | 11,9 | 1,6 | 0 | 82 | 45,2 | 39,6 | 13 | 1,9 | 0,1 | 81 | 43 | 40,3 | 14,2 | 2,2 | 0,1 | 80 | 40,9 | 40,9 | 15,3 | 2,5 | 0,1 | 79 | 38,9 | 41,4 | 16,5 | 2,9 | 0,1 | 78 | 37 | 41,7 | 17,6 | 3,3 | 0,2 | 77 | 35,1 | 42 | 18,8 | 3,7 | 0,2 | 76 | 33,3 | 42,1 | 19,9 | 4,2 | 0,3 | 75 | 31,6 | 42,1 | 21 | 4,6 | 0,3 | 74 | 29,9 | 42,1 | 22,2 | 5,2 | 0,4 | 73 | 28,3 | 42 | 23,3 | 5,7 | 0,5 | 72 | 26,8 | 41,8 | 24,3 | 6,3 | 0,6 | 71 | 25,4 | 41,5 | 25,4 | 6,9 | 0,7 | 70 | 24 | 41,1 | 26,4 | 7,5 | 0,8 | 69 | 22,6 | 40,7 | 27,4 | 8,2 | 0,9 | 68 | 21,3 | 40,2 | 28,4 | 8,9 | 1 | 67 | 20,1 | 39,7 | 29,3 | 9,6 | 1,1 | 66 | 18,9 | 39 | 30,2 | 10,3 | 1,3 | 65 | 17,8 | 38,4 | 31 | 11,1 | 1,5 | 64 | 16,7 | 37,7 | 31,8 | 11,9 | 1,6 | 63 | 15,7 | 37 | 32,6 | 12,7 | 1,8 | 62 | 14,7 | 36,2 | 33,3 | 13,6 | 2 | 61 | 13,8 | 35,4 | 33,9 | 14,4 | 2,3 | 60 | 12,9 | 34,5 | 34,5 | 15,3 | 2,5 | 59 | 12,1 | 33,6 | 35,1 | 16,2 | 2,8 | 58 | 11,3 | 32,7 | 35,6 | 17,1 | 3,1 | 57 | 10,5 | 31,8 | 36 | 18,1 | 3,4 | 56 | 9,8 | 30,9 | 36,4 | 19 | 3,7 | 55 | 9,1 | 29,9 | 36,7 | 20 | 4,1 | 54 | 8,5 | 28,9 | 37 | 21 | 4,4 | 53 | 7,8 | 27,9 | 37,2 | 22 | 4,8 | 52 | 7,3 | 26,9 | 37,3 | 23 | 5,3 | 51 | 6,7 | 25,9 | 37,4 | 24 | 5,7 | 50 | 6,2 | 25 | 37,5 | 25 | 6,2 | От 0 до 50 таблица будет симметрична, относительно центра. К тому же при определении каждой дихотомии с точностью меньше 50% само типирование смысла не имеет, так как результат получается хуже, чем случайный. Метод определения типа с помощью признаков Рейнина Обычно при использовании признаков Рейнина имеется в виду, совпадение всех 15 или тех, которые конкретный типировщик считает надежными. Я предлагаю другой подход, а именно поиск наиболее подходящего ТИМа по количеству совпавших признаков Рейнина. Интуитивно понятно, что при использовании признаков Рейнина, надежность типирования должна повыситься. А вот вопрос насколько достаточно сложен. Для ответа на него построим математическую модель. Будем определять 15 признаков (4 основных дихотомии + 11 признаков Рейнина). Как и ранее делаются следующие предположения: 1. Признаки определяются независимо.
2. Для простоты рассмотрим случай, когда вероятности определение каждого из признаков равны между собой. Опять важно заметить, что не делается никаких предположений: - О распределении типов в природе.
- О конкретном психологическом наполнении каждого из признаков.
- О конкретном способе определения каждого из признаков.
Итак, у нас есть 15 независимых испытаний, каждый признак может принимать одно из значений: 0 или 1, таким образом получаем 215 = 32768 случаев. Каждый из 16 ТИМов можно записать в виде последовательности 15 нулей и единиц. Возьмем в качестве 1 – правильное определение признака, 0 – неправильное, вероятность правильного определения каждого признака p, вероятность неправильного определения q = 1 – p. Аналогично предыдущему случаю получаем биномиальное распределение. 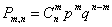 , где n = 15, m – количество верно определенных признаков. , где n = 15, m – количество верно определенных признаков.
Построим таблицу вероятностей в процентах по количеству правильно определенных признаков в зависимости от вероятности p определения каждого из признаков. (есть в полном варианте статьи) Запишем для каждого типа последовательность из 15 нулей и единиц, где они означают наличие или отсутствие определенного признака. Можно определить и посчитать расстояние между двумя числами, записанными в таком виде, как количество различных признаков, то есть количество 1 полученных после логической операции сложения по модулю 2 (xor). Будем считать результатом типирования ТИМ, у которого отличается минимальное число признаков Рейнина от полученного нами. Несложно заметить, что у любой пары типов из 15 признаков (4 основных дихотомий + 11 признаков Рейнина) 7 совпадают и 8 не совпадают. Таким образом, если мы получили от 12 до 15 правильно определенных признаков, то любой другой тип может набрать не больше, чем 15 – (8 - (15-12)) = 10 совпадающих признаков, а, значит, тип в данном случае будет определен однозначно и верно. Если мы получили 11 совпадающих признаков, то другие типы могут набрать не более 15 – (8 – (15-11)) = 11 совпадающих признаков, а значит, наш тип входит во множество типов с наибольшим количеством совпадающих признаков, но при этом он не обязательно является единственным ответом. При количестве верно определенных признаков меньше или равной 11 комбинаторная задача становится достаточно сложной, поэтому вместо того, чтобы решать на бумаге, я смоделировал ее на компьютере и посчитал все возможные варианты. Количество совпавших признаков | Количество типов с максимальным совпадением признаков | Количество вариантов, в которых присутствует верный тип в качестве результата | Всего вариантов с данным количеством совпавших признаков для верного типа | 15 | 1 | 1 | 1 | 14 | 1 | 15 | 15 | 13 | 1 | 105 | 105 | 12 | 1 | 455 | 455 | 11 | 1 | 420 | 1365 | 11 | 2 | 840 | 1365 | 11 | 3 | 105 | 1365 | 10 | 3 | 315 | 3003 | 10 | 4 | 1680 | 3003 | 10 | 6 | 168 | 3003 | 9 | 7 | 105 | 5005 | 9 | 10 | 280 | 5005 | 8 | 15 | 15 | 6435 | Вероятность правильного определения каждой дихотомии или признаку p | Вероятность
однозначного
определения правильного типа с помощью основных дихотомий | Вероятность однозначного
определения правильного типа с помощью основных дихотомий и признаков Рейнина | Вероятность определения вхождения правильного типа из двух с помощью основных дихотомий и признаков Рейнина | Вероятность определения вхождения правильного типа из трех с помощью основных дихотомий и признаков Рейнина | Вероятность определения вхождения правильного типа из четырех с помощью основных дихотомий и признаков Рейнина | 100 | 100 | 100 | 0 | 0 | 0 | 99 | 96 | 99,9 | 0 | 0 | 0 | 98 | 92,2 | 99,8 | 0 | 0 | 0 | 97 | 88,5 | 99,7 | 0 | 0 | 0 | 96 | 84,9 | 99,5 | 0,1 | 0 | 0 | 95 | 81,4 | 99,3 | 0,2 | 0 | 0 | 94 | 78 | 99 | 0,4 | 0 | 0 | 93 | 74,8 | 98,5 | 0,8 | 0,1 | 0,1 | 92 | 71,6 | 97,7 | 1,3 | 0,2 | 0,2 | 91 | 68,5 | 96,7 | 1,9 | 0,3 | 0,3 | 90 | 65,6 | 95,4 | 2,5 | 0,4 | 0,5 | 89 | 62,7 | 94 | 3,3 | 0,5 | 0,8 | 88 | 59,9 | 92,2 | 4,2 | 0,7 | 1,1 | 87 | 57,2 | 90,2 | 5,1 | 0,9 | 1,5 | 86 | 54,7 | 88,1 | 6 | 1,1 | 1,9 | 85 | 52,2 | 85,6 | 7 | 1,3 | 2,4 | 84 | 49,7 | 82,8 | 8 | 1,5 | 3 | 83 | 47,4 | 79,9 | 8,9 | 1,8 | 3,6 | 82 | 45,2 | 76,8 | 9,9 | 2 | 4,3 | 81 | 43 | 73,6 | 10,7 | 2,2 | 5 | 80 | 40,9 | 70,3 | 11,5 | 2,5 | 5,7 | 79 | 38,9 | 66,9 | 12,1 | 2,7 | 6,4 | 78 | 37 | 63,4 | 12,7 | 2,9 | 7,2 | 77 | 35,1 | 59,8 | 13,2 | 3,1 | 7,8 | 76 | 33,3 | 56,4 | 13,6 | 3,3 | 8,5 | 75 | 31,6 | 52,8 | 13,8 | 3,4 | 9,2 | 74 | 29,9 | 49,2 | 13,9 | 3,5 | 9,7 | 73 | 28,3 | 45,8 | 13,9 | 3,6 | 10,3 | 72 | 26,8 | 42,6 | 13,9 | 3,7 | 10,7 | 71 | 25,4 | 39,2 | 13,7 | 3,8 | 11,1 | 70 | 24 | 36,2 | 13,4 | 3,8 | 11,5 | 69 | 22,6 | 33,1 | 13 | 3,8 | 11,7 | 68 | 21,3 | 30,3 | 12,6 | 3,8 | 11,9 | 67 | 20,1 | 27,5 | 12,1 | 3,7 | 11,9 | 66 | 18,9 | 24,9 | 11,5 | 3,6 | 11,9 | 65 | 17,8 | 22,5 | 11 | 3,6 | 11,8 | 64 | 16,7 | 20,4 | 10,4 | 3,4 | 11,6 | 63 | 15,7 | 18,1 | 9,7 | 3,3 | 11,4 | 62 | 14,7 | 16,2 | 9,1 | 3,2 | 11,1 | 61 | 13,8 | 14,3 | 8,4 | 3 | 10,7 | 60 | 12,9 | 12,6 | 7,7 | 2,9 | 10,3 | 59 | 12,1 | 11,1 | 7,1 | 2,7 | 9,9 | 58 | 11,3 | 9,8 | 6,5 | 2,5 | 9,4 | 57 | 10,5 | 8,6 | 5,9 | 2,4 | 8,8 | 56 | 9,8 | 7,3 | 5,2 | 2,2 | 8,3 | 55 | 9,1 | 6,3 | 4,7 | 2 | 7,8 | 54 | 8,5 | 5,6 | 4,2 | 1,8 | 7,2 | 53 | 7,8 | 4,7 | 3,7 | 1,7 | 6,7 | 52 | 7,3 | 3,9 | 3,3 | 1,5 | 6,1 | 51 | 6,7 | 3,3 | 2,8 | 1,4 | 5,5 | 50 | 6,2 | 2,8 | 2,5 | 1,2 | 5 | Таким образом, наглядно показано насколько применение признаков Рейнина дает большую точность типироваия в зависимости от точности определения каждого признака. При 63% и ниже метод использования дихотомий дает даже большую точность, чем предложенный, но так как вероятность правильного определения ТИМа все равно ниже 20%, то в данном случае это неважно. Сравнение методов 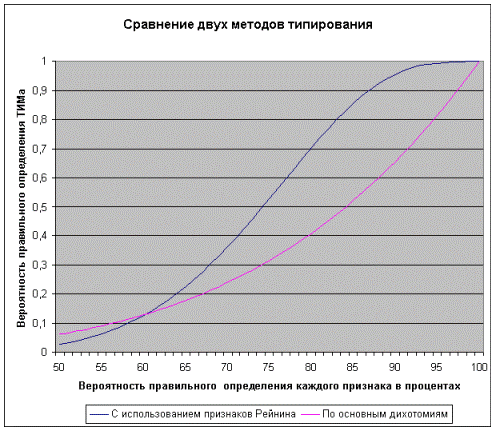
6. Замечание Вернемся к нашим предположениям. 1. Признаки строятся так, как предлагал Григорий Рейнин. В психике, к сожалению или к счастью, не все так просто как в математике, поэтому предположение о том, что хотя бы основные дихотомии образуют базис, находится под большим вопросом. Кроме того, выделение пятнадцати пар признаков гораздо сложнее, чем четырех. Наполнение признаков Рейнина таким образом, чтобы они соответствовали модели, то есть один превалировал над другим у восьми конкретных ТИМов, а у остальных восьми все было бы наоборот, кажется мне очень сложной задачей. Первые шаги в этом направлении сделаны, насколько они удачны, покажет будущее. 2. Признаки определяются независимо. Это очень важно, так как иначе будет подгон под свою версию, в психике всегда присутствует как одно качество, так и его противоположность, а значит всегда можно выделить некоторый контекст, в котором проявится не превалирующий признак. 3. Для простоты рассмотрим случай, когда вероятности определение каждого из признаков равны между собой. Если мы знаем, что вероятность определения некоторых признаков у нас выше чем других, то можно модифицировать вышеприведенный метод, добавив корректирующие коэффициенты, то есть ввести веса конкретных признаков. 4. Не делается никаких предположений о распределении типов в природе. То есть при использовании предлагаемого метода нам не важно распределены ТИМы равномерно или нет, важна лишь точность определения каждого признака. 5. Не делается никаких предположений о конкретном психологическом наполнении каждого из признаков и о конкретном способе определения каждого из признаков. А значит, это дает нам свободу в поиске этого наполнения и выбора наиболее адекватного способа для определения каждого признака. Допустим один из признаков можно определить с помощью интервью, другой – по семантике, третий – активностью определенных зон головного мозга и так далее. На основе предложенного метода можно создать новый соционический тест определения ТИМа, дающий более точный результат, чем те, которые используют только четыре основных дихотомии. В будущем данный метод можно усовершенствовать, добавив к нему анализ по модели А Литература 1. Григорий Рейнин «Группа биполярных признаков в типологии Карла Юнга». 2. Аушра Аугустинавичюте «Теория признаков Рейнина». 3. Виктор Таланов «Экспериментальное исследование признаков Рейнина (по материалам тестов ЛОТ и Холланда)». Полный вариант статьи здесь
|